√10x+1+√4y+12=2的函数性质图像
1、 函数的定义域,根据函数特征,结合根式要求为非负数,即可求出函数的定义域,本题函数的定义域最终为一个闭区间。

2、通过函数的一阶导数,求出函数驻点,由一阶导数的正负,判断函数的单调性,进而得到函数的单调区间。

3、函数导数的应用,求曲线上点的切线方程,举例介绍如下。
例如求点A(-110,21)处的切线。
解:由导数y'=-52*4y+1210x+1 可知,
当x=-110时,导数不存在。
所以此时函数的切线方程为:x=-110。

4、例如求点B(310,-3)处的切线和法线方程。
解:此时导数y'=-52*4y+1210x+1 =-4*3+1210*310+1 =0,
则此时函数y的切线为y=-3,
法线方程为:x=310。

5、根据根式函数性质,求出函数的值域。y它代表函数图象上每一个点的纵坐标的数值,因此函数图像上所有点的纵坐标构成一个集合,这个集合就是函数的值域。

6、变形根式表达式,由根式为非负数,解出值域也为一闭区间。
根据函数单调性,则当x0=3/10时,
该函数有最小值,将x0代入隐函数有:
√(10*3/10+1)+√(4y+11)=2,
2+√(4y+11)=2,即4y+11=0,
则y=-11/4为所求隐函数的最小值。
同时:
对函数√(10x+1)+√(4y+11)=2有:
√(4y+11)=2-√(10x+1)≤2,
不等式两边同时平方为:
4y+11≤4,即:
4y≤-7,则y≤-7/4,
综合求出该隐函数的值域为:
[-11/4, -7/4]。

7、通过求解函数的二次导数,判定函数图像的凸凹性。如果函数f(x)在区间I上二阶可导,则f(x)在区间I上是凸函数的充要条件是f''(x)<=0。

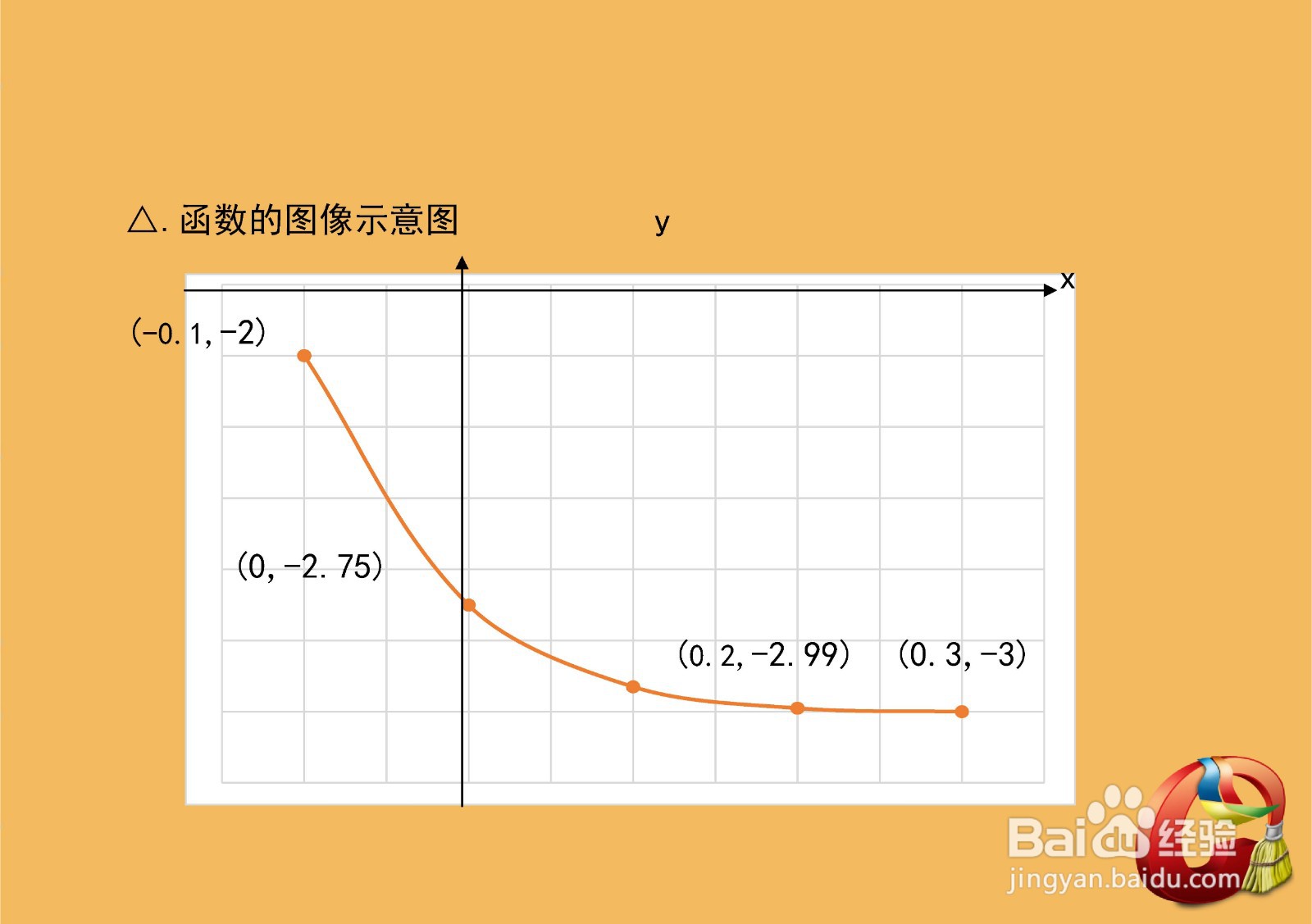
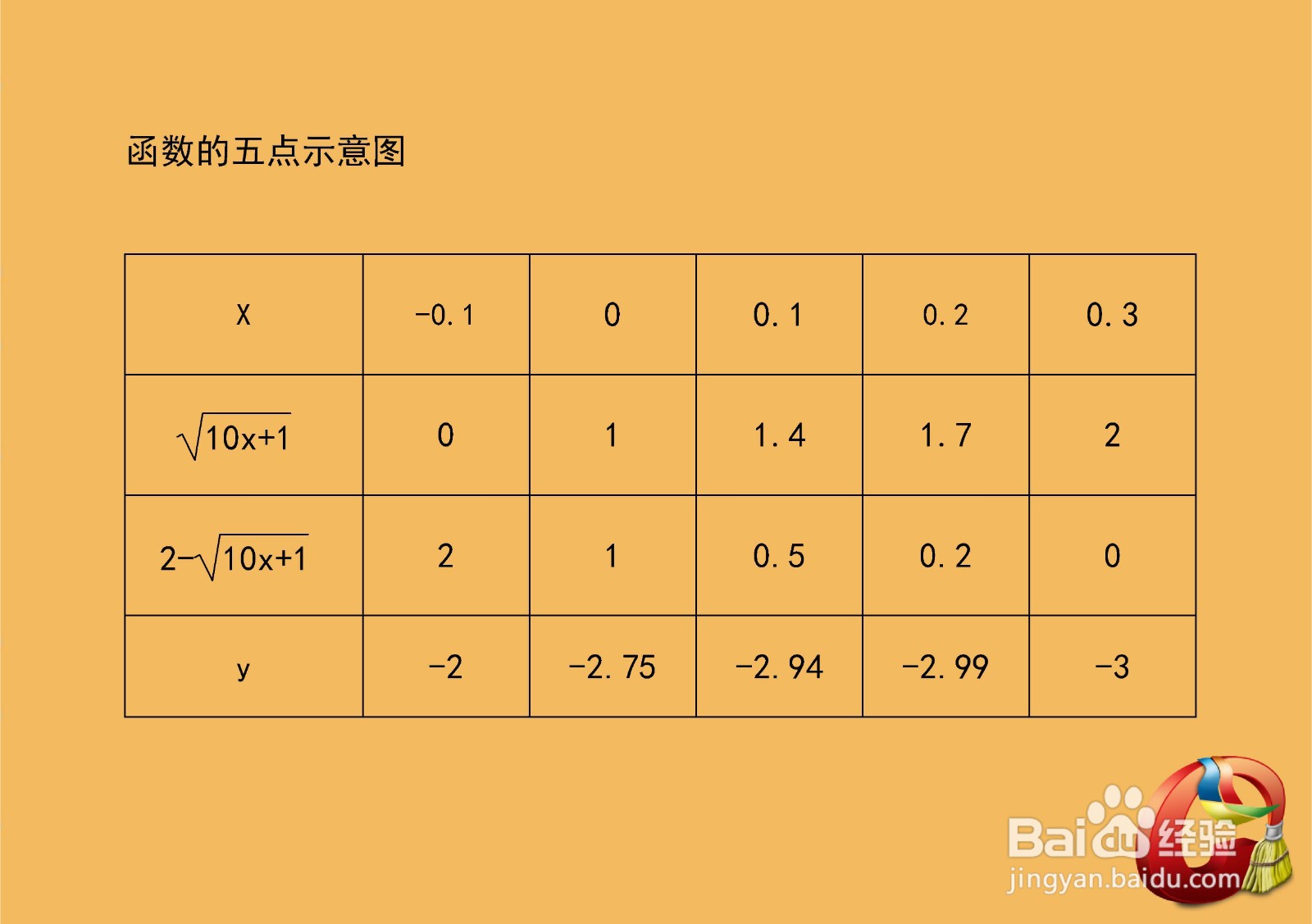
8、函数图像五点示意图,列图表解析函数上的五点图如下表所示。
9、综合以上函数的相关性质,结合函数的定义域,即可简要画出函数的示意图。