Mathematica基础——处理连分数问题
Mathematica不仅可以处理各种数学方程,还可以给出数字漂亮的根式解!下面,就来学习一下相关函数和代码!

工具/原料
电脑
Mathematica
基本函数
1、ContinuedFraction[Pi, 20]——求圆周率π的 连分数展开式的前20项。我们可以把它化简为分式的形式:FromContinuedFraction[ContinuedFraction[Pi, 20]]结果是:14885392687/4738167652。

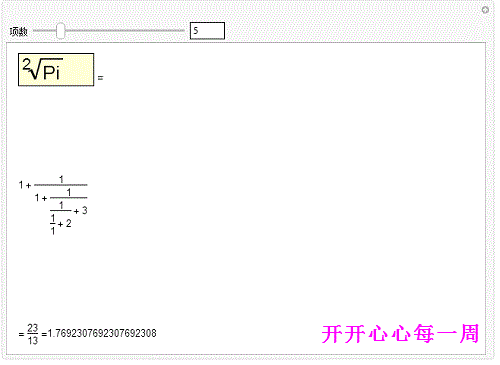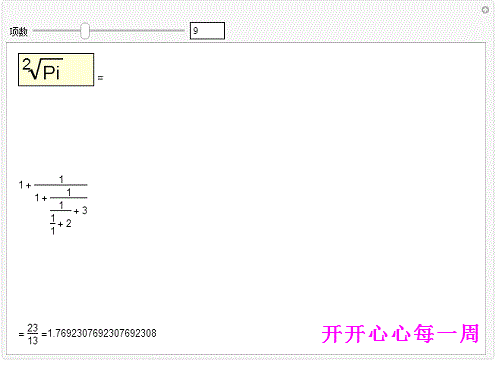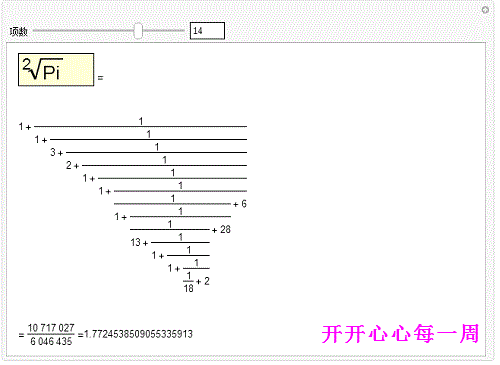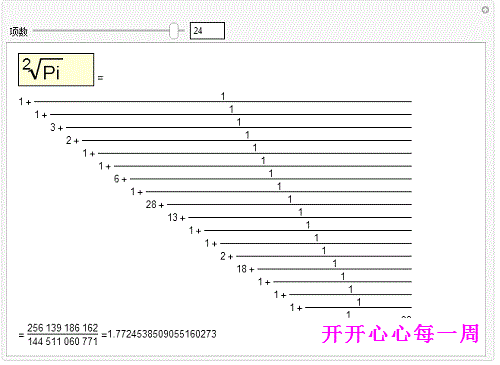
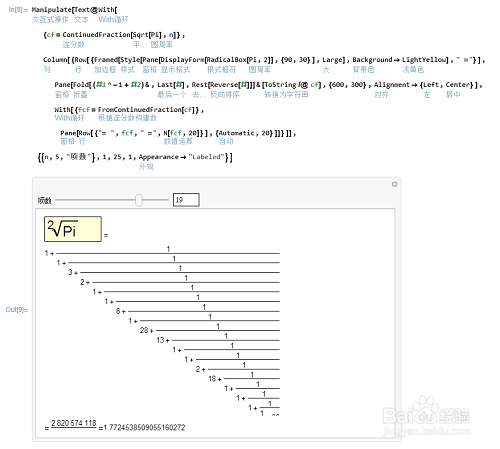
2、用一些辅助函数,可以写出 π的传统的连分数形式,并且还可以手动控制它的项数:Man坡纠课柩ipulate[Text@With缪梨痤刻[{cf=ContinuedFraction[Sqrt[Pi],n]},Column[{Row[{Framed[Style[Pane[DisplayForm[RadicalBox[Pi,2]],{90,30}],Large],Background->LightYellow]," ="}],Pane[Fold[(#1^-1+#2)&,Last[#],Rest[Reverse[#]]]&[ToString/@cf],{600,600},Alignment->{Left,Center}],With[{fcf=FromContinuedFraction[cf]},Pane[Row[{"= ",fcf," =",N[fcf,20]}],{Automatic,20}]]}]],{{n,5,"项数"},1,25,1,Appearance->"Labeled"}]但是,好像最后面那一部分没能完整显示!
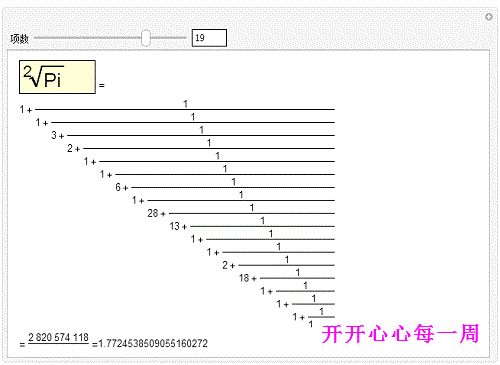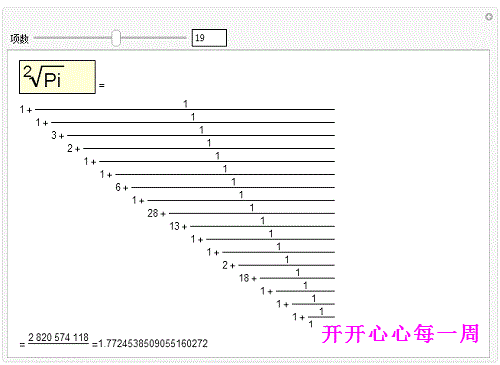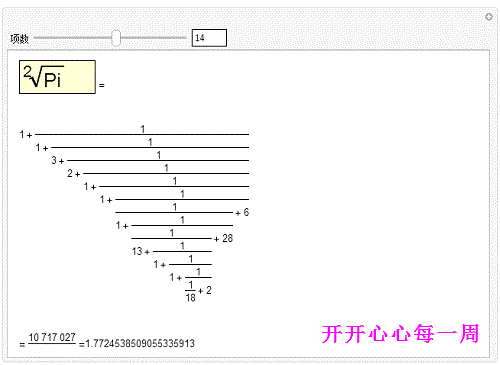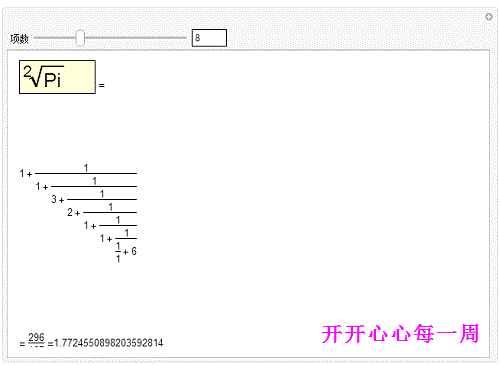
代码分析——写出π的连分数
1、ContinuedFraction是“连分数”的意思,给出数字的连分数展开式的简化形式。但是,这跟我们平时看到的连分数外形相差很大 。From潮贾篡绐ContinuedFraction是“来自连分数 ”的意思,就是把连分数化简为分式形式。下面,我们一步一步地来分析上面这段代码!首先,把ContinuedFraction[Sqrt[Pi],n]的结果定义为cf,把fcf=FromContinuedFraction[cf]的结果定义为fcf。注意:cf和fcf定义里面的参数n是变量,因此,cf和fcf要整合的With循环内部,否则代码不能运行!
2、RadicalBox是“根号盒子”的意思,就是我们常说的根号。但是,下面的代码没什么意义 :RadicalBox[Pi,1]

3、要想看到正确的根式符号,需要“展示”——DisplayForm:DisplayForm[RadicalBox[Pi,2]]结果如图。

4、Pane,是“格子、窗格”的意思!我们用格子把式子包起来,但是格子默认是透明的,所以,看起来没什么效果!但是,实际上是不同的,你只要用鼠标“选中”运行结果,就能看出区别!代码里面的{Automatic,60}表示格子的大小——宽度自定、高度为60.Pane[DisplayForm[RadicalBox[Pi,1]],{Automatic,60}]

5、我们可以改变格子里面内容的大小(由于里面是以文本形式存在的,所以,用Style来约束它):Style[Pane[DisplayForm[RadicalBox[Pi,1]]{Automatic,30}],Large]

6、我们可以给这个格子加上背景色(Background),再套上一个外框(Frame),这样看起来就不会有空洞感了!同时,在格子右边加一个“=”,使格子和等号保持在同一行,这就要用的Row——行!看下图,格子的背景色设置为浅黄色。从第二步到第六部 ,就是给出了这个根号式和后面的等号。这是第一个格子。

7、再来处理连分数的主题部分——第二个格子。先把cf变成字符串,用到的函数是ToString,代码如下:ToString/@cf你能看出它与cf本身有什么区别吗?看不出来!但是,这一步处理却是必须的。原因稍后就知道。

8、用Fold函数给出连分数:Fold[(#1^-1+#2)&,Last[#],Rest[Reverse[#]]]&[ToString/@cf]对比一下:Fold[(#1^-1+#2)&,Last[#],Rest[Reverse[#]]]&[cf],就知道,cf有没有必要作字符串处理了。

9、再把这个连分数放到一个格子里,格子大小是600*300.Pane[Fold[(#1^-1+#2)&,Last[#],Rest[Reverse[#]]]&[ToString/@cf],{600,300}]这样,π的连分数也放到格子里了。

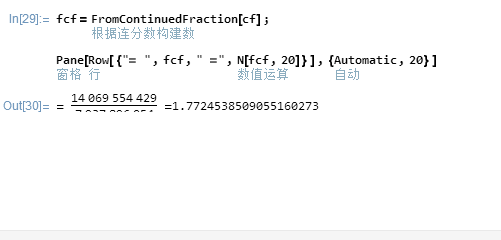
10、下面是第三个格子——化简连分数、化为小数形式。fcf=FromContinuedFraction[cf];Pane[Row[{"= ",fcf," =",N[fcf,20]}],{Automatic,20}]其中,N[fcf,20]就是在“化为小数形式”。可是,我们发现,分式显示不完整,原来是格子太小了 ,我们可以让格子的宽和高都Automatic。

11、现在,三个格子都做好了,可以用Column排成一列:Column[{Row[{Framed[Style[Pane[DisplayForm[RadicalBox[Pi,2]],{90,30}],Large],Background->LightYellow]," ="}],Pane[Fold[(#1^-1+#2)&,Last[#],Rest[Reverse[#]]]&[ToString/@cf],{600,300},Alignment->{Left,Center}],With[{fcf=FromContinuedFraction[cf]},Pane[Row[{"= ",fcf," =",N[fcf,20]}],{Automatic,Automatic}]]}]三个格子,对应三段代码,最后用Column整合!
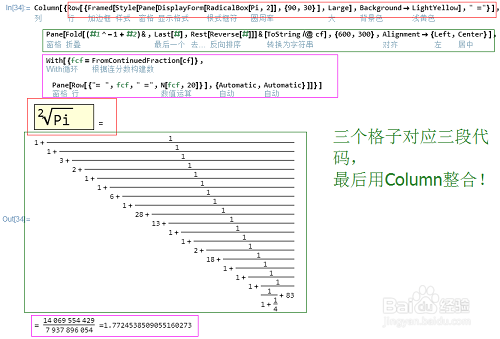
最后的效果
1、最后,经过对代码的理解,可以给出下面效果较好的互动代码!Manipulate[Text@With[{cf=ContinuedFract足毂忍珩ion[Sqrt[Pi],n]},Column[{Row[{Framed[Style[Pane[DisplayForm[RadicalBox[Pi,2]],{90,30}],Large],Background->LightYellow]," ="}],Pane[Fold[(#1^-1+#2)&,Last[#],Rest[Reverse[#]]]&[ToString/@cf],{600,300},Alignment->{Left,Center}],With[{fcf=FromContinuedFraction[cf]},Pane[Row[{"= ",fcf," =",N[fcf,20]}],{Automatic,Automatic}]]}]],{{n,5,"项数"},1,25,1,Appearance->"Labeled"}]但还是显示的不完整 ,大家可以自己调整格子的大小!