函数极限计算法宝之一——泰勒公式

1、泰勒公式的核心问题就是究竟展开到哪一项，具体规则如下：1、如果是a/b类型，则展开到上下同阶2、如果是a-b类型，则展开到最低阶的那个不为0的项

2、比如这一题，分子就是a-b类型，整体是a/b类型，故根据上述规则，e^x*sinx要展开到x的3次阶。

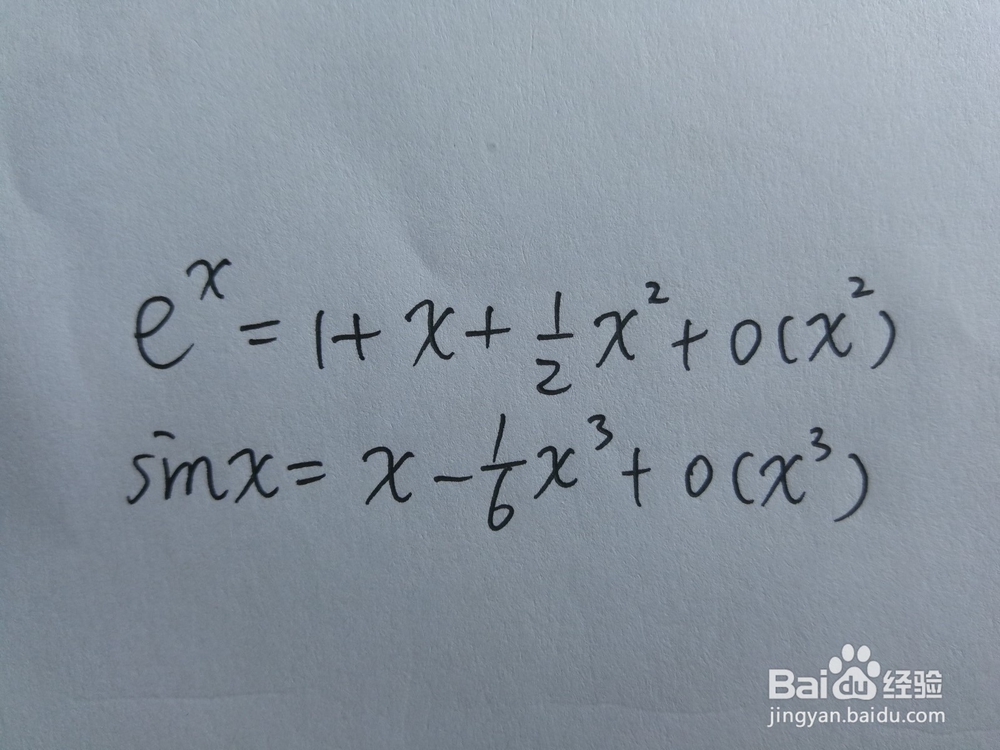
4、如此一来，上题的具体步骤如图所示。

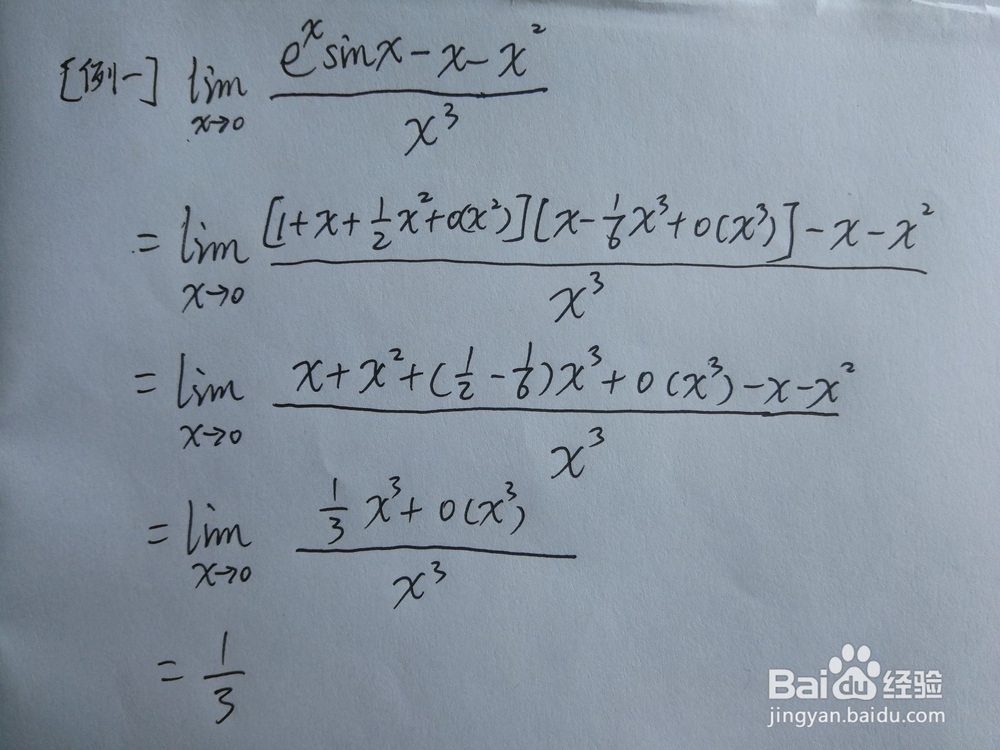
5、泰襻唛嵋膑勒公式对比洛必达法则，优点在于，它不要求分子分母可导，而且通过展开式能迅速找到两个无穷小之间的差异，但是缺点在于，泰勒公式只能用于未知数趋于0的情况，洛必达可以是趋于无穷大。对于复杂的极限计算，熟练运用泰勒公式往往能迅速确定结果，洛必达需要一步一步求导，也就是一阶一阶地降阶，通常更加复杂。泰勒公式在后面的中值定理中也有广泛的应用。