极坐标下的二次曲线方程
1、椭圆x^2/5^2+y^2/3^2=1的极坐标方程是:ρ=1 / sqrt((cos(t) ^ 2 )/ 25 + (sin(t) ^ 2) / 9)

2、绘图:PolarPlot[xxx[[2]]/.{a->5,b->3},{t,0,2 Pi}]

3、椭圆(x-p)^2/a^2+(y-q)^2/b^2=1对应的极坐标方程,可以用Solve求出来:Solve[(ρ*Cos[t]-p)^2/a^2+(ρ*Sin[t]-q)^2/b^2==1,ρ]

4、如果令p=1,q=0.5,a=5,b=3,对应的极坐标方程是:xxx[[2]]/.{p->1,q->1/2,a->5,b->3}

5、对应的图像如下,注意看坐标轴的位置。

6、双曲线x^2/5^2-y^2/3^2=1对应的极坐标方程是:ρ=15/sqrt(17*cos(2*t)-8)图像如下:

7、(x-p)^2/a^2-(y-q)^2/b^2=1对应的极坐标方程,可以用Mathematica求出来:so造婷用痃l0=Solve[(ρ*Cos[t]-p)^2/a^2-(ρ*Sin[t]-q)^2/b^2==1,ρ]xxy=\[Rho]/.sol0//FullSimplifyxxy[[2]]xxy[[1]]

8、当p=1,q=0.5,a=5,b=3时,双曲线对应的极坐标方程很复杂,但是图像却很简单,只不过出现了渐近线,不知道为什么。


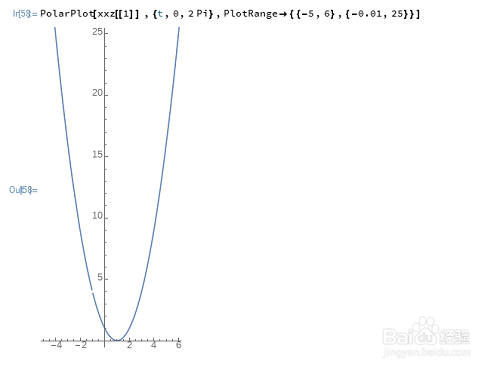
9、y=x^2-2*x+1的极坐标方程是:ρ=(Sec[t]*(4+Sec[t]*Sqrt[2-2*Cos[2*t]+8*Sin[2*t]]+Tan[2*t]))/2

10、绘制图像:PolarPlot[xxz[[1]] ,{t,0,2 Pi},PlotRange->{{-5,6},{-0.01,25}}]
11、看看(x+y+1)*(x-y+1)=0对应的图像:ContourPlot[(x+y+1) (x-y+1)==0 ,{x,-5,5},{y,-3.65,3.65}】这是两条直线。

12、双直线(x+y+1)*(x-y+1)=0的极坐标方程可以求解:sol2=Solve[(x+鲻戟缒男y+1) (x-y+1)==0 /.{x->ρ Cos[t],y->ρ Sin[t]},ρ]结果,两条直线的极坐标方程竟然自动分离开来了,解方程解出来两个解,恰好分别是两条直线的极坐标方程。图像如下:PolarPlot[{ρ/.sol2[[1]],ρ/.sol2[[2]]},{t,0,2 Pi}]

13、如果ρ/.sol2不经过Evaluate,图形就有点不知所谓:PolarPlot[ρ/.sol2,{t,0,2 Pi}]对比一下:PolarPlot[ρ/.sol2//Evaluate,{t,0,2 Pi}]
