过单位圆外（2,5）割线中点轨迹方程

1、 介绍用轨迹性质法等介绍由圆x^2+y^2=1外一点p（2,5）引圆的割线交圆于A、B两点，求弦AB的中点M的轨迹方程。

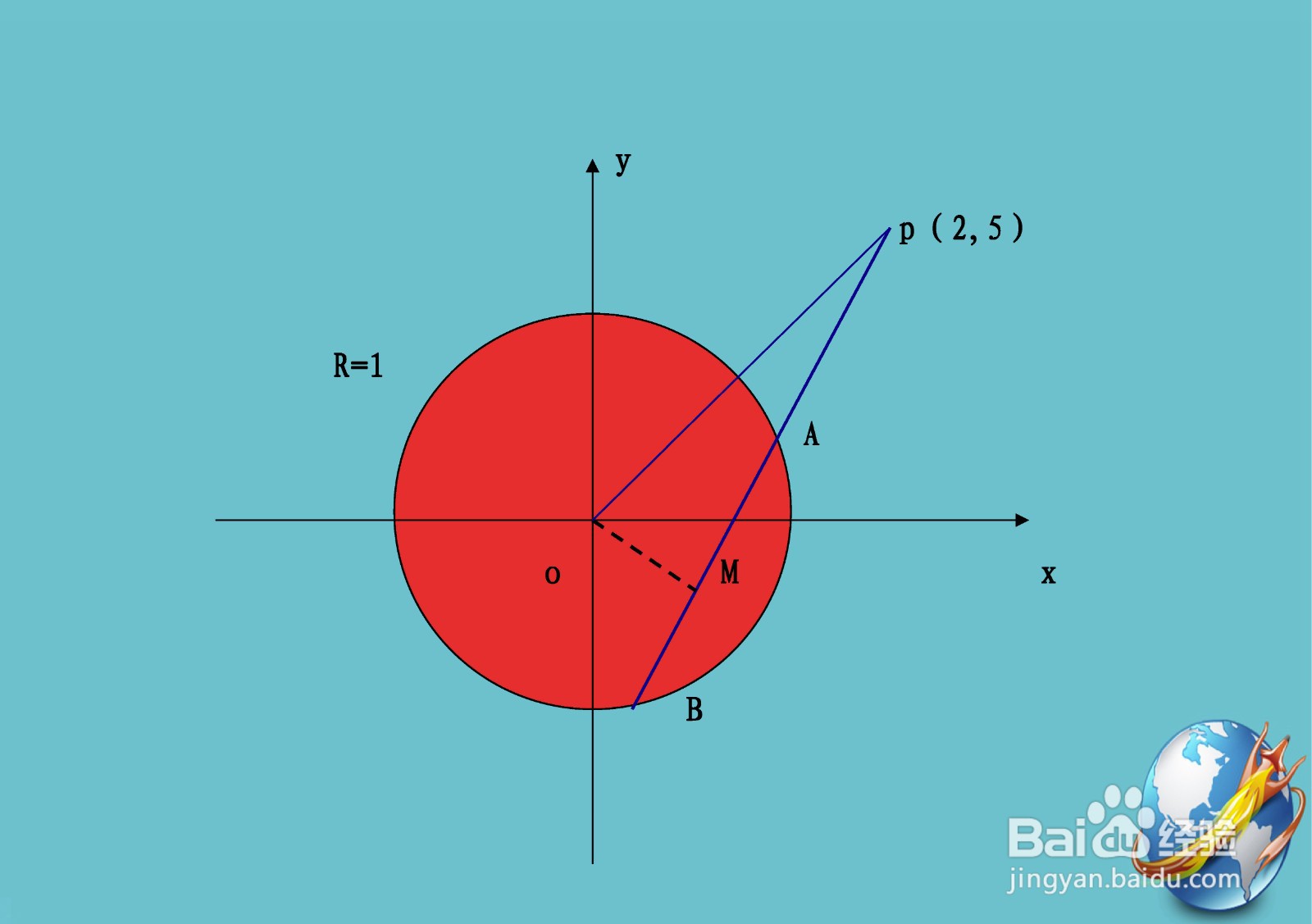
3、根据题设条件列出几何等式，运用解析几何基本公式转化为代数等式，并根据在圆中有关弦中点的一些性质，圆心和弦中点的连线垂直于弦，从而求出轨迹方程。

6、方法四：参数求轨迹法将动点坐标表示成某一中间变量即参墙绅褡孛数的函数，再设法消去参数。由于动点M(xi,y足毂忍珩i)随直线的斜率变化而发生变化，所以动点M的坐标是直线斜率的函数。解：设过P点的割线方程为：y-5=k(x-2), 它与圆x2+y2=R2的两个交点为A、B，AB的中点为M.解方程组:y-5=k(x-2),x2+y2=1消去y得：x2+(kx-2k+5)2=1,即： (1+k2)x2-2k(2k-5)x+(5-2k)2-1=0,

7、yi[1+(xiyi)2]=5+2*xiyi,化简得：yi(yi2+xi2)=5yi2+2xiyiyi2+xi2=5yi+2xi,即所求的轨迹方程为：x2+y2-2x-5y=0,其中：-1≤x≤1.

9、解：设M(x,y),A(x1,y1),B猾诮沓靥(x2,y2),则:x1+x2=2x,y1+y2=2y，∵x12+y12=1，x22+y22=1，两式减得：(x2-x1)(x2+x1)+烫喇霰嘴(y2-y1)(y1+y2)=0,即：y2-y1x2-x1 =-x2+x1y2+y1=-xy ；即为AB的斜率，而AB对斜率又可表示为5-y2-x,即：5-y2-x =-xy，化简得：y(5-y)+x(2-x)=0,即所求轨迹方程为：x2+y2-2x-5y=0,其中：-1≤x≤1.